- Créer un projet dans ce dossier :
- Bien réfléchir au nom de ce projet
- Bien réfléchir à l’endroit où ce projet sera situé
- Créer un script
- Savoir où sont les données, et sous quel format
- Savoir ce que l’on veut faire !
Bien se préparer à coder
C’est parti pour les commandes de base !
Le(s) prompt(s)
>: R attend une commande à exécuter+: la commande qui a été entrée n’est pas complète car- il manque une parenthèse fermante
- il manque un crochet fermant
- il manque une accolade fermante
: la commande est en cours de traitement. On peut l’arrêter en cliquant sur le bouton “Stop”
Une commande, c’est quoi ?
C’est une séquence d’opérations appliquées à des objets ou des valeurs qui sera donnée au compilateur de R pour interprétation.
- “opération” : permet de transformer des entrées en sorties, p.ex. : la fonction
log; - “objets” : structures de données, p.ex. : plus tard ;
- “valeurs” : des briques de base, p.ex. : la valeur
0.
Une fois la commande écrite dans la console, on l’exécute en appuyant sur “Entrée”.
Exercice
Exécutez les commandes suivantes :
1 + 11+1log(10)log10(10)
Remarquez l’utilisation des parenthèses pour appliquer une fonction !
Opérations de base
On peut effectuer toutes les opérations de base en R :
- addition (
+), soustraction (-), multiplication (*), division (/), exponentiation (**ou^)…
appliquer les fonctions mathématiques de base :
- logarithme (
log,log2,log10), exponentielle (exp) sinus (sin), cosinus (cos), tangente (tan)
On peut combiner les opérations et les fonctions, et gérer les priorités avec des parenthèses !
Exercice
Imaginez une commande incluant le plus d’opérations et de fonctions de base et dont le résultat serait 2 !
Un opérateur bien pratique, le :
Comment créer une suite d’entier ?
c(1, 2, 3, 4)seq(1, 4, 1)1:4
L’opérateur : est très utilisé en R. Sa syntaxe est la suivante
- \(i\)
:\(j\) va créer une suite d’entiers de \(i\) à \(j\). Les entiers peuvent être négatifs ou positifs, et on peut peut avoir \(i < j\) ou \(i > j\), ou même \(i = j\).
Attention à bien mettre des parenthèses dans le cas d’entiers négatifs!
Exemples
3:7: les entiers de 3 à 77:3: les entiers de 7 à 3-3:7: les entiers de -3 à 7-3:-7: les entiers de -3 à -7-(3:7): les entiers de -3 à -7
Exercice
- Créez un vecteur d’entiers de 0 à 3
- Créez un autre vecteur d’entiers de 3 à 1
- Combinez ces deux suites pour obtenir le vecteur suivant :
| 3 | 2 | 1 | 0 | 1 | 2 | 3 |
Assignation avec <-
Comment “sauvegarder” ces objets ?
En utilisant l’opérateur d’assignation
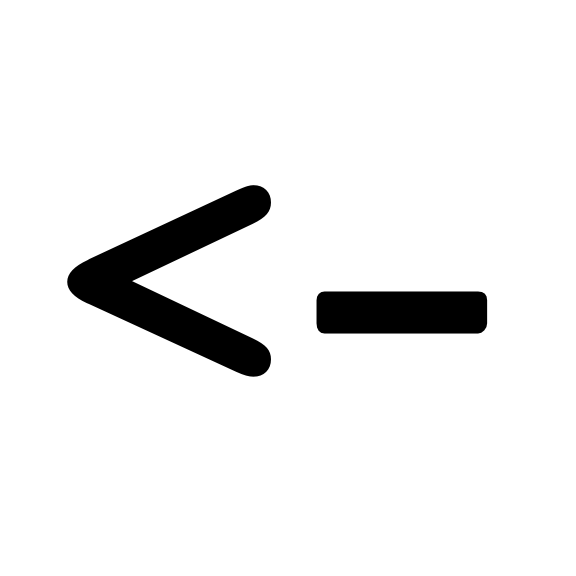
Utilisation de l’opération d’assignation
- A gauche : l’objet que l’on veut créer
- A droite : sa définition
- Lecture de l’opération : “assigner à cet objet (à gauche) le résultat de cette commande (à droite)”
- Assigner deux fois de suite écrasera la première valeur assignée
- Alternative :
= - Exemples :
a <- 1; b <- 1:10; a <- 2etc.
Les noms d’objets
Règles absolues :
- Commence par une lettre ou un point, si le premier caractère est un point, le deuxième ne peut pas être un chiffre,
- Pas d’espace
- Pas de caractères correspondant à des opérations (
+,-,*,/,^,**, etc.) - Les minuscules et les majuscules sont différentes !
- Certains “mots-clefs” sont strictement interdits (
NA,TRUE,FALSE,for,if,elseetc.) - MAIS on peut utiliser un nom d’objet qui existe déjà !
Bonnes pratiques :
- Utiliser un nom qui a du sens
- Ne pas utiliser des noms d’objets qui existent déjà et que l’on ne souhaite pas écraser !
Mini exercice
- Créez un vecteur d’entiers de 0 à 3, appelez le
a - Créez un autre vecteur d’entiers de 3 à 1, appelez le
b - Combinez ces deux vecteurs pour obtenir un vecteur
abselon le modèle suivant :
| 3 | 2 | 1 | 0 | 1 | 2 | 3 |
Opérations
On peut appliquer des opérations à ces “vecteurs” !
a <- 1:5 a + 1 #> [1] 2 3 4 5 6 a * 2 #> [1] 2 4 6 8 10
Ces “vecteurs” sont des objets.
Les Objets
Classes d’objets
| Nom | Appelation officielle | Exemple |
|---|---|---|
| Vecteur | ??? | 1:10 |
| Facteur | factor |
gl(2, 2) |
| Matrice | matrix |
matrix(1:4, 2, 2) |
| Tableau | data.frame |
mtcars |
| Liste | list |
list(a = 1, b = 1:10, c = "Hello!") |
| Fonction | function |
sin, exp, log |
Pour connaître la classe d’un objet : class(objet).
Types de données
| Nom | Appellation officielle | Exemple |
|---|---|---|
| Entier (\(\mathbb Z\)) | integer |
1:10, (ou 1L) |
| Réel (\(\mathbb R\)) | double |
2.3, 1/3, etc… |
| Caractères | character |
month.name, "Bonjour" |
| Booléen | logical |
TRUE |
Bouh les quoi ?
MATH., néol. Qui est relatif aux théories du logicien et mathématicien anglais George Boole.
– Trésor de la Langue Française informatisé
TRUE(ou bienT) etFALSE(ou bienF)- Résultat d’une comparaison :
==,!=,<,>,<=,>= - Opérations logiques :
!,&,|,xor
Exercice
- Effectuez les opérations suivantes :
1 == 2!(5 > -6)(1 <= 10) | (1 > 0)
Prédisez le résultat de la commande suivante : log(1) != 0
“Classification” des objets
Les objets qui ne contiennent qu’un seul type de données : vecteurs et matrices.
Les objets pouvant contenir des données mixtes : tableaux et listes.
La flexibilité a un coût : on ne peut plus faire certaines opérations !
Les objets ayant des “dimensions” : vecteurs, tableaux et matrices
Les objets pour qui cela ne signifie rien ou presque : listes et fonctions
Petit détour par les tableaux
data("fruits", package = "minidebuter")
dim(fruits)
#> [1] 51 18
nrow(fruits)
#> [1] 51
ncol(fruits)
#> [1] 18
Juste le début de la table
head(fruits)
#> nom groupe Energie Eau Proteines Glucides Lipides Sucres Fructose Fibres #> 1 Abricot crus 194 87.1 0.81 9.01 0.25 6.7 1.3 1.7 #> 2 Abricot secs 1010 24.7 2.88 59.10 0.50 34.3 10.6 8.3 #> 3 Ananas exotique 304 81.3 0.94 15.10 0.25 14.9 2.8 2.4 #> 4 Banane exotique 383 75.8 1.06 19.70 0.25 15.6 3.8 2.7 #> 5 Canneberge secs 1410 14.6 0.25 76.40 1.00 72.8 28.4 5.7 #> 6 Cerise crus 235 85.7 0.81 13.00 0.25 10.0 4.6 1.6 #> Calcium Magnesium Phosphore Potassium Zinc BetaCarotene VitamineE VitamineC #> 1 15.0 8.4 22.0 260 0.09 2350.0 0.70 2.55 #> 2 71.0 41.0 79.0 1400 0.35 2160.0 5.52 0.25 #> 3 6.3 15.0 9.6 130 0.11 21.2 0.04 18.30 #> 4 5.1 28.0 29.0 320 0.14 28.5 0.04 7.16 #> 5 8.0 3.9 7.5 58 0.05 15.5 1.92 0.25 #> 6 9.9 8.8 19.0 190 0.06 242.0 0.04 4.09
Toute la table
fruits
#> nom groupe Energie Eau Proteines Glucides Lipides Sucres #> 1 Abricot crus 194 87.1 0.81 9.01 0.25 6.70 #> 2 Abricot secs 1010 24.7 2.88 59.10 0.50 34.30 #> 3 Ananas exotique 304 81.3 0.94 15.10 0.25 14.90 #> 4 Banane exotique 383 75.8 1.06 19.70 0.25 15.60 #> 5 Canneberge secs 1410 14.6 0.25 76.40 1.00 72.80 #> 6 Cerise crus 235 85.7 0.81 13.00 0.25 10.00 #> 7 Citron crus 118 91.3 0.25 1.56 0.25 0.80 #> 8 Clementine crus 200 87.0 0.81 9.17 0.25 8.60 #> 9 CompoteMultiFruits compote 279 82.9 0.25 15.30 0.08 14.60 #> 10 CompotePomme compote 432 72.9 0.23 24.40 0.21 20.70 #> 11 Figue crus 293 80.2 1.19 13.50 0.25 12.20 #> 12 Fraise crus 162 90.3 0.63 6.03 0.25 5.60 #> 13 Framboise crus 206 86.8 1.19 5.83 0.80 5.40 #> 14 FruitCru crus 251 84.5 0.70 11.60 0.26 9.89 #> 15 Grenade crus 340 79.4 1.44 14.30 1.20 13.30 #> 16 Groseille crus 289 82.1 1.56 7.06 0.70 6.63 #> 17 Kaki exotique 290 81.8 0.88 14.30 0.25 13.90 #> 18 Kiwi exotique 255 83.5 0.88 11.00 0.60 8.90 #> 19 Lime exotique 170 86.3 1.13 3.14 0.25 2.10 #> 20 Litchi exotique 344 80.5 1.13 16.10 0.25 15.70 #> 21 Mangue exotique 376 77.1 0.75 19.30 0.50 18.40 #> 22 Maracuja exotique 425 73.6 2.13 10.90 3.00 8.50 #> 23 Melange secs 1640 11.7 2.19 69.50 10.50 59.40 #> 24 Melon crus 265 84.2 1.13 14.80 0.25 10.60 #> 25 Mirabelle crus 325 78.1 0.63 18.00 0.25 13.30 #> 26 Mure crus 198 86.1 1.13 6.53 0.70 6.10 #> 27 Myrtille crus 244 84.2 0.87 10.60 0.33 9.96 #> 28 NectarineBlanche crus 220 86.5 0.81 11.40 0.25 8.90 #> 29 NectarineJaune crus 218 86.6 0.69 11.30 0.25 8.80 #> 30 Orange crus 192 87.3 0.75 8.03 0.25 7.60 #> 31 Pamplemousse crus 169 89.3 0.25 8.02 0.25 6.60 #> 32 Papaye exotique 178 88.8 0.75 8.53 0.25 8.10 #> 33 Papaye exotique 169 88.6 0.56 7.88 0.25 7.70 #> 34 Pasteque crus 165 91.0 0.69 8.33 0.25 7.90 #> 35 PecheBlanche crus 199 87.6 0.69 9.48 0.25 8.70 #> 36 PecheBlanche crus 195 87.6 0.63 9.63 0.25 7.80 #> 37 PecheJaune crus 196 87.8 0.69 9.80 0.25 7.60 #> 38 PoireConference crus 223 85.3 0.25 11.40 0.25 9.40 #> 39 PoireWilliams crus 228 84.7 0.25 11.50 0.25 9.40 #> 40 PommeGolden crus 242 85.1 0.25 12.80 0.25 11.50 #> 41 PommeChantecler crus 219 86.4 0.25 11.20 0.25 10.80 #> 42 PommeGala crus 230 85.5 0.25 11.90 0.25 11.10 #> 43 PommeGrannySmith crus 217 85.8 0.25 10.70 0.25 10.10 #> 44 PommePinklady crus 254 83.6 0.25 12.80 0.25 12.30 #> 45 Prune crus 301 80.1 0.94 16.40 0.25 10.40 #> 46 Pruneau secs 969 34.9 1.63 55.40 0.40 38.10 #> 47 PureeDeFruits compote 249 84.2 0.25 13.40 0.25 11.30 #> 48 Raisin secs 1360 16.0 3.00 73.20 0.90 70.30 #> 49 RaisinBlanc crus 311 80.9 0.75 16.60 0.25 15.50 #> 50 RaisinChasselas crus 335 79.4 0.75 16.90 0.50 16.50 #> 51 RaisinNoirMuscat crus 381 76.7 0.69 20.00 0.25 19.60 #> Fructose Fibres Calcium Magnesium Phosphore Potassium Zinc BetaCarotene #> 1 1.30 1.70 15.00 8.40 22.0 260 0.090 2350.00 #> 2 10.60 8.30 71.00 41.00 79.0 1400 0.350 2160.00 #> 3 2.80 2.40 6.30 15.00 9.6 130 0.110 21.20 #> 4 3.80 2.70 5.10 28.00 29.0 320 0.140 28.50 #> 5 28.40 5.70 8.00 3.90 7.5 58 0.050 15.50 #> 6 4.60 1.60 9.90 8.80 19.0 190 0.060 242.00 #> 7 0.40 0.25 11.00 7.90 12.0 140 0.330 2.50 #> 8 1.50 1.70 23.00 9.30 18.0 140 0.100 147.00 #> 9 6.92 1.60 6.20 5.50 11.0 140 0.050 99.30 #> 10 7.90 1.53 4.44 5.09 6.0 104 0.025 3.00 #> 11 6.20 4.10 57.00 22.00 21.0 230 0.160 73.60 #> 12 3.30 3.80 18.00 12.00 23.0 140 0.110 2.50 #> 13 2.80 4.30 16.00 20.00 29.0 170 0.240 100.00 #> 14 3.62 1.97 14.50 12.10 20.1 197 0.110 314.00 #> 15 7.10 2.30 9.50 12.00 27.0 230 0.220 12.10 #> 16 3.86 4.60 38.00 12.00 38.0 230 0.150 25.60 #> 17 6.40 3.40 6.90 7.20 13.0 160 0.050 180.00 #> 18 4.30 2.40 29.00 12.00 26.0 290 0.120 38.00 #> 19 0.80 4.30 57.00 14.00 24.0 190 0.150 12.40 #> 20 8.10 2.00 3.60 18.00 27.0 200 0.230 2.50 #> 21 8.65 1.80 14.00 14.00 13.0 150 0.080 2010.00 #> 22 2.50 6.80 8.10 26.00 46.0 240 0.760 1010.00 #> 23 19.50 3.40 43.00 39.00 67.0 530 0.320 13.60 #> 24 2.49 1.30 11.00 16.00 17.0 380 0.180 2500.00 #> 25 2.20 2.20 11.00 8.20 21.0 240 0.110 346.00 #> 26 3.08 5.20 31.00 20.00 25.0 200 0.180 156.00 #> 27 4.97 2.40 6.00 6.00 12.0 77 0.160 32.00 #> 28 1.30 0.25 5.00 8.10 18.0 210 0.100 2.50 #> 29 1.20 0.60 4.80 8.00 19.0 220 0.110 144.00 #> 30 2.10 2.70 66.00 15.00 38.0 180 0.250 2.50 #> 31 1.90 0.80 14.00 7.20 17.0 140 0.070 539.00 #> 32 4.10 1.80 22.00 18.00 8.7 200 0.050 351.00 #> 33 3.60 2.20 18.00 12.00 11.0 240 0.090 1230.00 #> 34 3.60 0.50 6.00 11.00 9.7 100 0.090 1220.00 #> 35 0.90 2.10 4.10 7.10 18.0 180 0.110 2.50 #> 36 0.80 1.10 3.90 6.80 18.0 170 0.100 2.50 #> 37 1.10 1.00 4.20 6.70 17.0 190 0.090 130.00 #> 38 6.60 3.10 3.90 5.30 9.3 99 0.070 19.30 #> 39 7.20 3.10 6.10 5.30 9.8 120 0.090 2.50 #> 40 6.90 1.40 4.00 3.80 10.0 130 0.070 56.00 #> 41 5.40 1.90 4.00 3.60 10.0 120 0.050 54.60 #> 42 6.30 1.90 3.60 3.00 7.8 91 0.050 11.60 #> 43 5.80 2.80 3.20 2.80 7.6 110 0.050 11.60 #> 44 6.60 2.90 2.80 3.00 7.5 110 0.050 32.30 #> 45 1.80 1.70 13.00 9.50 20.0 250 0.120 430.00 #> 46 12.50 5.10 50.00 30.00 66.0 610 0.280 14.90 #> 47 7.20 1.70 6.20 6.00 11.0 140 0.050 31.00 #> 48 36.00 4.20 54.00 35.00 82.0 960 0.240 2.50 #> 49 8.50 1.00 12.00 7.60 16.0 200 0.050 7.54 #> 50 8.40 2.00 16.00 7.50 21.0 150 0.070 27.40 #> 51 9.80 2.70 13.00 7.30 20.0 210 0.060 67.70 #> VitamineE VitamineC #> 1 0.70 2.55 #> 2 5.52 0.25 #> 3 0.04 18.30 #> 4 0.04 7.16 #> 5 1.92 0.25 #> 6 0.04 4.09 #> 7 0.04 45.00 #> 8 0.21 49.20 #> 9 0.53 11.50 #> 10 0.18 14.50 #> 11 0.04 0.25 #> 12 0.30 54.00 #> 13 0.88 18.70 #> 14 0.29 20.90 #> 15 0.04 9.02 #> 16 1.19 29.80 #> 17 0.12 3.41 #> 18 0.96 81.90 #> 19 0.45 29.30 #> 20 0.04 19.20 #> 21 1.96 2.90 #> 22 0.50 25.60 #> 23 0.69 0.69 #> 24 0.04 8.14 #> 25 1.52 5.29 #> 26 1.28 10.10 #> 27 0.57 9.70 #> 28 1.04 3.01 #> 29 0.04 3.38 #> 30 0.19 47.50 #> 31 0.04 42.40 #> 32 0.04 65.30 #> 33 0.22 68.00 #> 34 0.04 4.26 #> 35 0.19 3.85 #> 36 0.28 4.09 #> 37 0.50 3.43 #> 38 0.04 1.39 #> 39 0.04 2.57 #> 40 0.04 0.25 #> 41 0.04 2.85 #> 42 0.04 1.33 #> 43 0.04 2.31 #> 44 0.04 2.13 #> 45 1.20 4.16 #> 46 0.41 0.25 #> 47 0.40 16.70 #> 48 1.67 0.25 #> 49 0.31 1.07 #> 50 0.35 4.14 #> 51 0.99 3.11
Importer des données en R
- Des données de packages :
data - Des données au format R (
RData) :load - Des données “tabulées” :
read.table - Des données Excel :
readxl::read_excel - Des données Stata, SPSS, images etc.
Les données “de R”
- Utiliser la commande
data()pour avoir une liste (presque ?) exhaustive. - Bonne pratique : pour charger un jeu de données, utiliser la commande complète
data("nom_des_data", package = "nom_du_package") - Mais ces alternatives fonctionnent également :
data(mtcars)DNaselibrary(ggplot2) ; data(diamonds)
Utilisation des guillemets
- Obligation : quand l’argument doit être une chaîne de caractères
- Oubli :
library,require,data - Guillemets simples : fonctionnent comme les guillemets doubles. Ex.:
"bonjour"est équivalent à'bonjour'. - Le “backtick” ou “backquote” : “`”
Explorer les données fruits
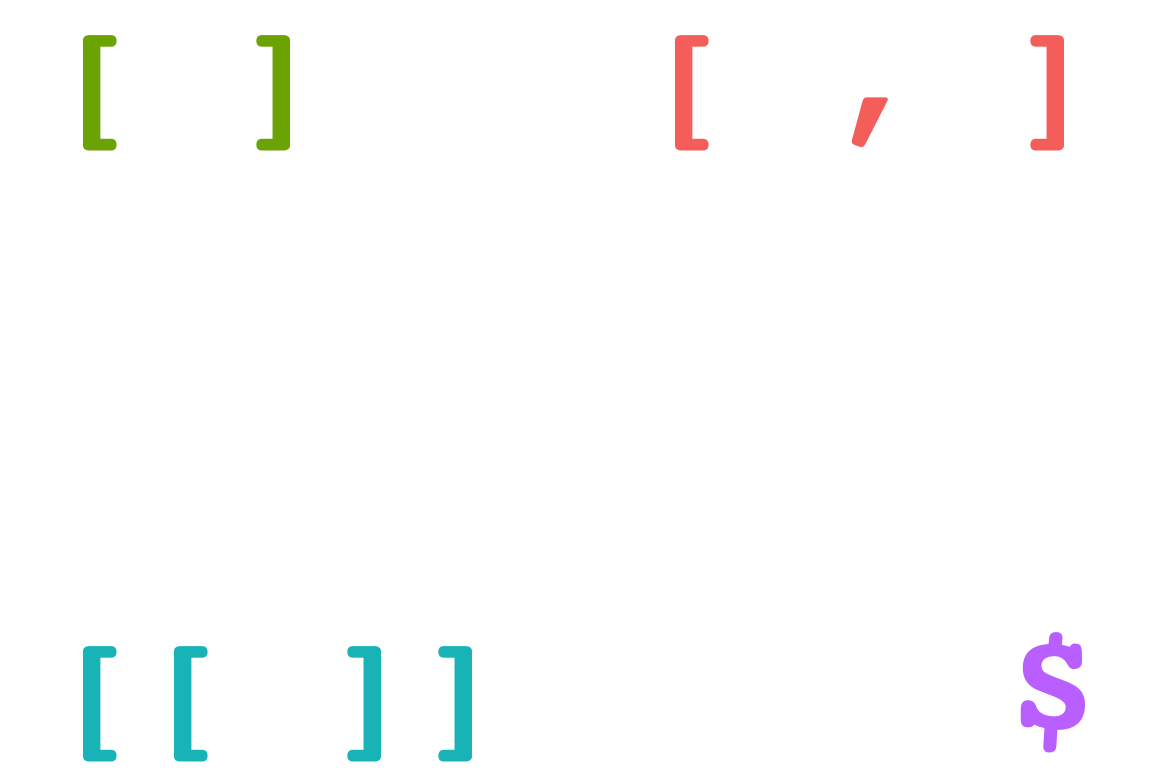
Sur quels objets les utiliser ?
| Opérateur | Vecteurs | Matrices | Tableaux | Listes |
|---|---|---|---|---|
[ ] |
x | x | x | |
[ , ] |
x | x | ||
[[ ]] |
x | x | ||
$ |
x | x |
L’opérateur de sélection classique : [ , ]
- Pour sélectioner la première ligne :
fruits[1, ] - Pour sélectionner la deuxième colonne :
fruits[, 2] - Pour enlever la troisième ligne :
fruits[-3, ] - Pour enlever la quatrième colonne :
fruits[, -4]
Exercice
Comment faire pour sélectionner les fruits numéro 1, 3 et 5 ?
Je veux deux solutions : une “normale” et une “créative” !
Sélectionner plusieurs lignes / colonnes
- Pour sélectioner les lignes 1 et 3 :
fruits[c(1, 3), ] - Pour sélectionner les colonnes 2 et 4 :
fruits[, c(2, 4)] - Pour enlever les lignes 5 et 7 :
fruits[-c(5, 7), ] - Pour enlever les colonnes 6 et 8 :
fruits[, -c(6, 8)]
De l’utilité des deux points
Pour sélectionner une plage entière de lignes ou de colonnes adjacentes :
- Pour sélectionner les lignes 11 à 17 :
fruits[11:17, ] - Pour sélectionner les colonnes 3 à 5 :
fruits[, 3:5] - Pour enlever les trois premiers fruits :
fruits[-(1:3), ] - Pour enlever les cinq premières variables :
fruits[, -(1:5)]
Exercice
Que se passe-t-il quand on oublie les parenthèses dans la commande fruits[-(1:3), ] ? Commentez !
Faites de même avec le jeu de données mtcars.
Pour extraire une seule colonne : le $
La syntaxe donnees$cible permet de sélectionner la colonne cible du tableau donnees.
- Par exemple :
fruits$Eau - Autre exemple :
fruits$groupe
N.B: la selection de la colonne sert soit à récupérer le contenu de cette colonne soit à créer la colonne ou remplacer son contenu. Par exemple : fruits$num <- 1:nrow(fruits)
Exercice
Extrayez la colonne de la teneur en sucres de la table des fruits… de deux façons différentes !
Créez un objets contenant la teneur en sucres : quelle est la classe de cet objet ?
Les vecteurs…
- … sont “unidimensionnels”
- … ont une classe qui est égale au type de données qu’ils contiennent (R !!!)
- … sont indexés avec des crochets simples
Exemples :
i <- 1:10eau <- fruits$Eaueau[i]
Exercice
Créez un vecteur groupe contenant les groupes de fruits. Donnez deux façons différentes d’extraire les dix premières valeurs de ce vecteur.
Extraction avec des Booléens
Comment extraire les fruits … * dont la teneur en eau est supérieure à 60 ? * exotiques ? * secs contenant moins de 40g/100g de sucres ?
Réponse : en utilisant des vecteurs booléens
- Créer le vecteur de booléens
fruits$Eau >= 60 - Utiliser le résultat dans les crochets carrés
fruits[fruits$Eau >= 60, ]
Ne pas oublier la virgule !
Le principe
Pour un vecteur v :
v[bool]extrait les valeurs devpour lesquellesboolest vrai (TRUE). Contrainte :vetbooldoivent contenir le même nombre d’élements.
Pour un tableau tab :
tab[brow, ]pour extraire les lignestab[, bcol]- Contrainte 1 :
browdoit avoir autant d’éléments quetabde lignes - Contrainte 2 :
bcoldoit avoir autant d’éléments quetabde colonnes
Attention
Vous verrez souvent des opérations logiques à l’intérieur des crochets carrés : cela permet d’aller plus vite !
Par exemple, en deux étapes :
bool <- fruits$groupe == "secs" & fruits$Sucres < 40fruits[bool, ]
Devient, en une étape :
fruits[fruits$groupe == "secs" & fruits$Sucres < 40, ]
Attention bis
On peut combiner deux méthodes d’extraction de données pour un tableau : une sur les lignes et une sur les colonnes !
Par exemple : tab[brow, icol], où brow est un vecteur de booléens et icol un vecteur d’indices.
Exercice
Construisez la sous-table contenant la teneur en protéines, en glucides et en lipides des fruits secs.
Les objets nommés
En R, on peut donner des “noms”…
- aux éléments d’un vecteur,
- aux lignes d’un tableau ou d’une matrice,
- aux colonnes d’un tableau ou d’une matrice,
- aux éléments d’une liste
Pourquoi ? Pour pouvoir disposer d’une nouvelle méthode d’extraction de données !
Pour un tableau
On utilise :
rownames(tab)pour connaître le nom des lignescolnames(tab)pour connaître le nom des colonnes
Et, en bonus, on peut :
- changer les noms des lignes
rownames(tab) <- new1 - changer les noms des colonnes
colnames(tab) <- new2
Et, en super bonus, on peut :
- modifier quelques noms de lignes
rownames(tab)[sel1] <- new1 - modifier quelques noms de colonnes
colnames(tab)[sel1] <- new2
Modifier un objet ou son contenu
La syntaxe obj[i] <- newvalue (et ses variations) peut être utilisée pour tous les types d’objets indiçables. Mais il faut l’utiliser avec prudence !
Exemple : fruits$Energie[1:10] <- 0
Que s’est-il passé ? Au secours !!!!
Pour revenir en arrière : data("fruits", package = "minidebuter")
Extraction avec des noms
Exemple :
- Pour extraire l’énergie :
fruits[, "Energie"], - Pour extraire le groupe :
fruits[, "groupe"], - Pour extraire l’énergie et le groupe :
fruits[, c("Energie", "groupe")], - Pour enlever le groupe :
fruits[, -"groupe"]?
Bilan
| Mode d’extraction | Exemples |
|---|---|
| Indices | fruits[, 2] |
| Booléens | fruits[fruits$nom == "Abricot", ] |
| Noms | fruits$nom ou fruits[,"nom"] |
Exercice
Lister le maximum de façons possibles d’extraire du tableau fruits les fruits crus sucrés riches en Vitamine C !
Construire ses propres objets
Vecteurs et facteurs
- La fonction
c()permet de combiner des valeurs dans un vecteur. Attention, tout doit être du même “type” ! - La fonction
seqpermet de créer des suites. - La fonction
reppermet de créer des vecteurs en répétant des valeurs. Ex:rep(c("a", "b"), c(3, 4))
Les facteurs sont une particularité de R !
- On les crée avec la fonction
factorouas.factor - Par exemple :
factor(fruits$groupe)
Matrices et tableaux
- Les fonctions
matrix,rbindetcbindpour créer des matrices. Attention, tout doit être du même “type” ! - Les fonctions
data.frameouas.data.framepour créer des tableaux, les colonnes ne contiennent pas nécessairement le même type de données. - Ou bien les fonctions
tibbleettribble(avancé)
Ajouter des noms
Directement à la création de l’objet. Ex: x <- c(a = 1, b = 2), d <- data.frame(a = 1:26, b = letters)
Ou bien après la création de l’objet :
names(obj) <- lesNomspour un vecteurrownames(obj) <- lesLignespour les lignes d’un tableau ou d’une matrice,colnames(obj) <- lesColonnespour les colonnes d’un tableau ou d’une matrice.
Exercice
Créez un facteur à partir des groupes de fruits, puis testez la commande suivante :
factor(fruits$groupe, levels = c("secs", "compote", "crus", "exotique"))
Que se passe-t-il ? Sauvez le résultat dans un objet et faites un diagramme en bâton avec ! Commentez !
Estimation ponctuelle
Définition
Il s’agit d’estimer un caractéristique statistique d’un ensemble de données avec une seule valeur.
| Paramètre | Grandeur statistique | Commande |
|---|---|---|
| Position | Moyenne | mean |
| Position | Médiane | median |
| Position | Minimum | min |
| Position | Maximum | max |
| Dispersion | Variance | var |
| Dispersion | Ecart-type | sd |
| Dispersion | Intervalle inter-quartiles | IQR |
| Lien | Covariance | cov |
| Lien | Corrélation | cor |
Rappel : la covariance
Permet de mesurer le degré de co-variation de deux variables :
\[ \operatorname{cov}(x, y)=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-m_{x}\right)\left(y_{i}-m_{y}\right) \]
Rappel : corrélation de Pearson
C’est une covariance normalisée entre -1 et 1 !
\[ \operatorname{cor}(x, y)=\frac{\operatorname{cov}(x, y)}{\sqrt{\operatorname{var}(x)} \sqrt{\operatorname{var}(y)}} \]
Rappel : corrélation de Spearman
C’est la corrélation (de Pearson) calculée sur les rangs !
\[
\rho = \operatorname{cor}(r_x, r_y),
\] avec \(r_x\) le vecteur des rangs de \(x\) (rank(x)), et \(r_y\) le vecteur des rangs de \(y\) (rank(y)).
Rappel (?) : corrélation de Kendall
- Paire concordante : \(\left(x_{i}<x_{j} \text { et } y_{i}<y_{j}\right)\) OU \(\left(x_{i}>x_{j} \text { et } y_{i}>y_{j}\right)\)
- Paire discordante : \(\left(x_{i}<x_{j} \text { et } y_{i}>y_{j}\right)\) OU \(\left(x_{i}>x_{j} \text { et } y_{i}<y_{j}\right)\)
\[ \tau = \displaystyle \frac{n_C - n_D}{n_0}, \] avec \(n_C\) le nombre de paires concordantes, \(n_D\) le nombre de paires discordantes et \(n_0\) le nombre total de paires de points.
Exercice
Calculez
- la médiane de la teneur en sucres
- la moyenne de la teneur en eau
- l’écart-type de la teneur en eau
Appliquez la fonction summary aux données fruits.
- Calculez la corrélation de Pearson entre la teneur en eau et la teneur en sucres,
- Calculez la corrélation de Spearman
Les fonctions astucieuses
summarypour obtenir des statistiquesstrpour la structure des donnéestablepour faire des tables de comptageseq_alongpour créer un vecteur d’indices de même longueur qu’un vecteur donné
D’autres fonctions très utilies
sumpour calculer la somme de nombressort,orderetrankpour ordonner, et calculer les rangsrowSumsetcolSumspour calculer les sommes des lignes et colonnes d’une table,rowMeansetcolMeanspour calculer les moyennes des lignes et colonnes d’une table,
Les graphes de base
barplot: diagrammes en bâtonshist: histogrammesplot: nuages de points
La fonction barplot
Permet de réaliser des diagrammes en bâtons :
barplot(table(fruits$groupe))
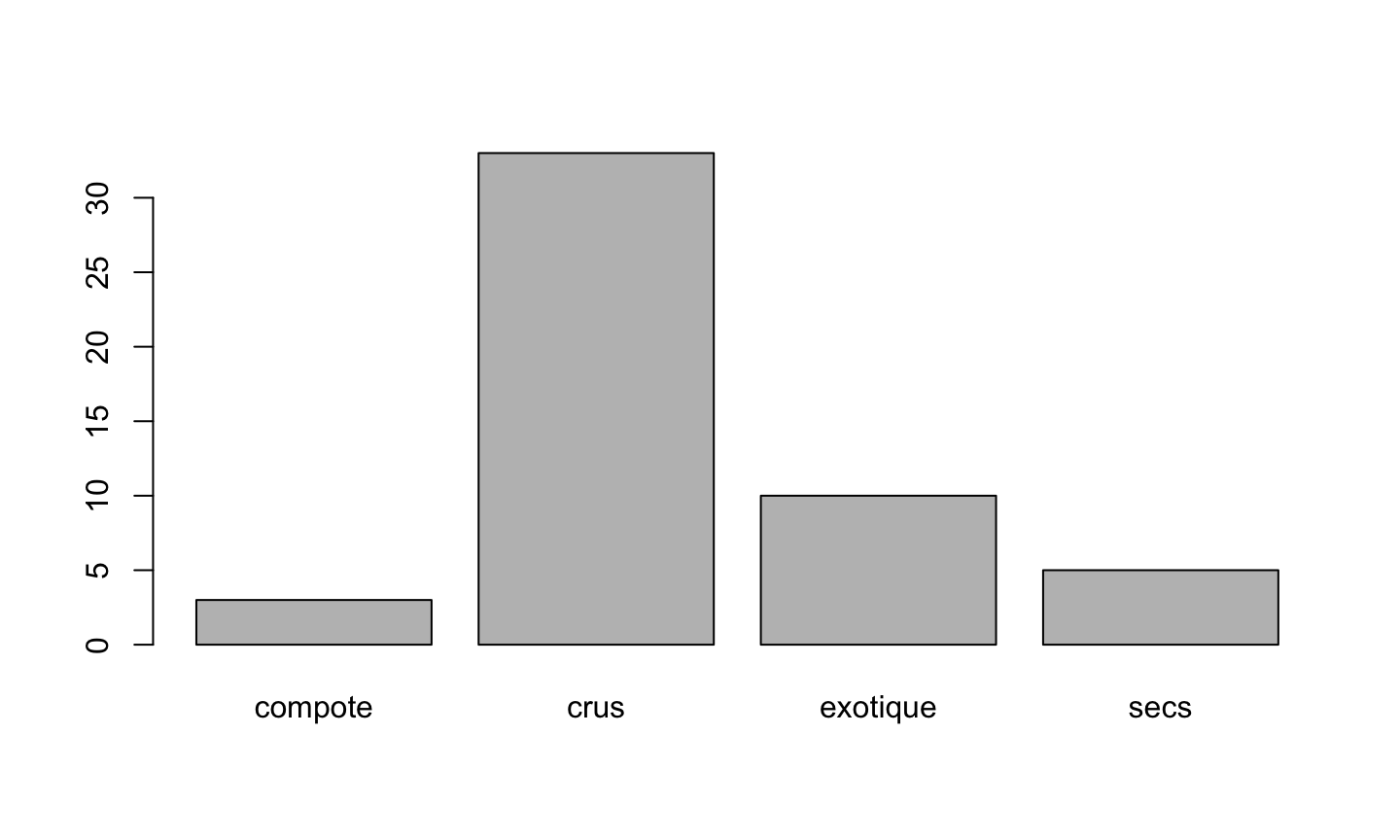
La fonction hist
Permet de réaliser des histogrammes :
hist(fruits$Eau)
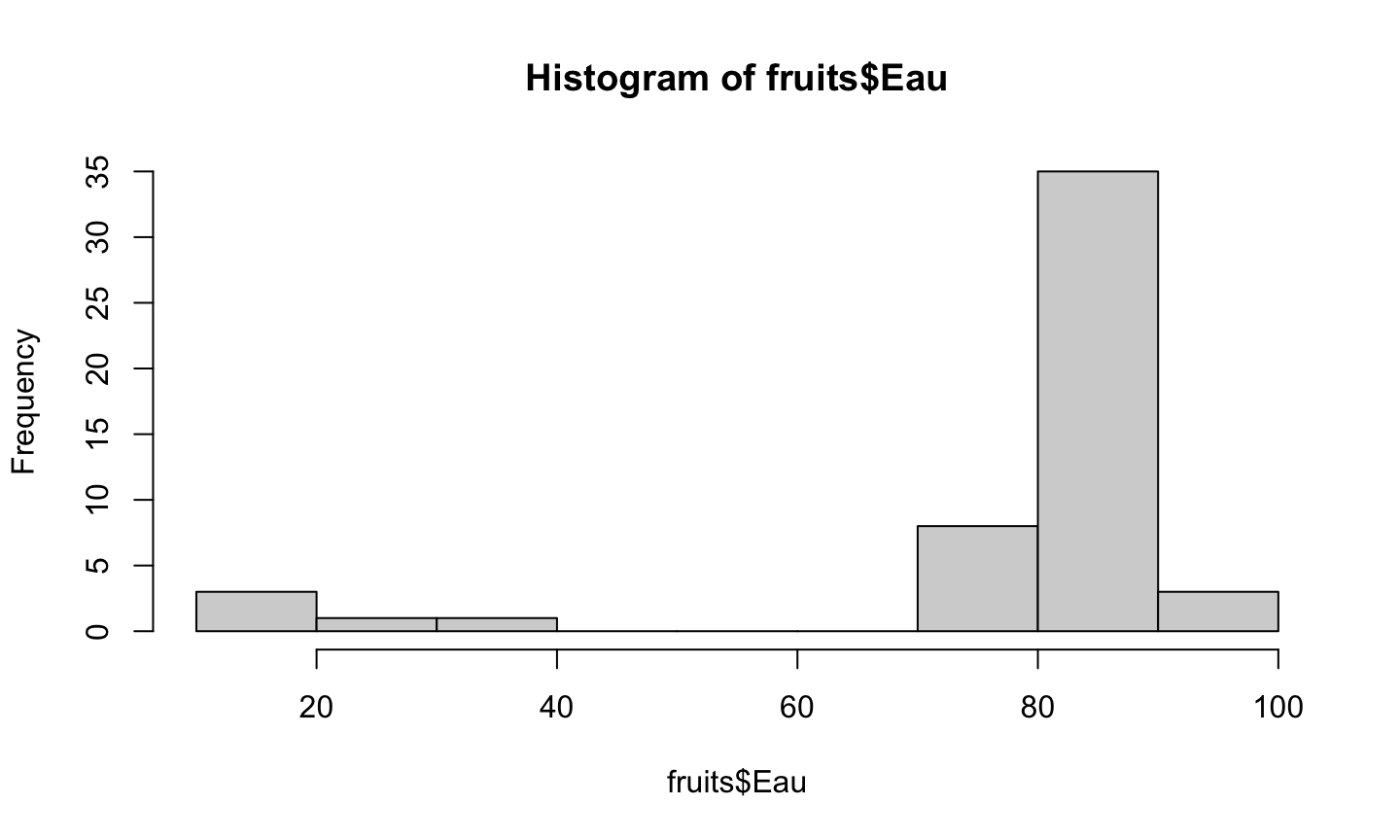
La fonction plot
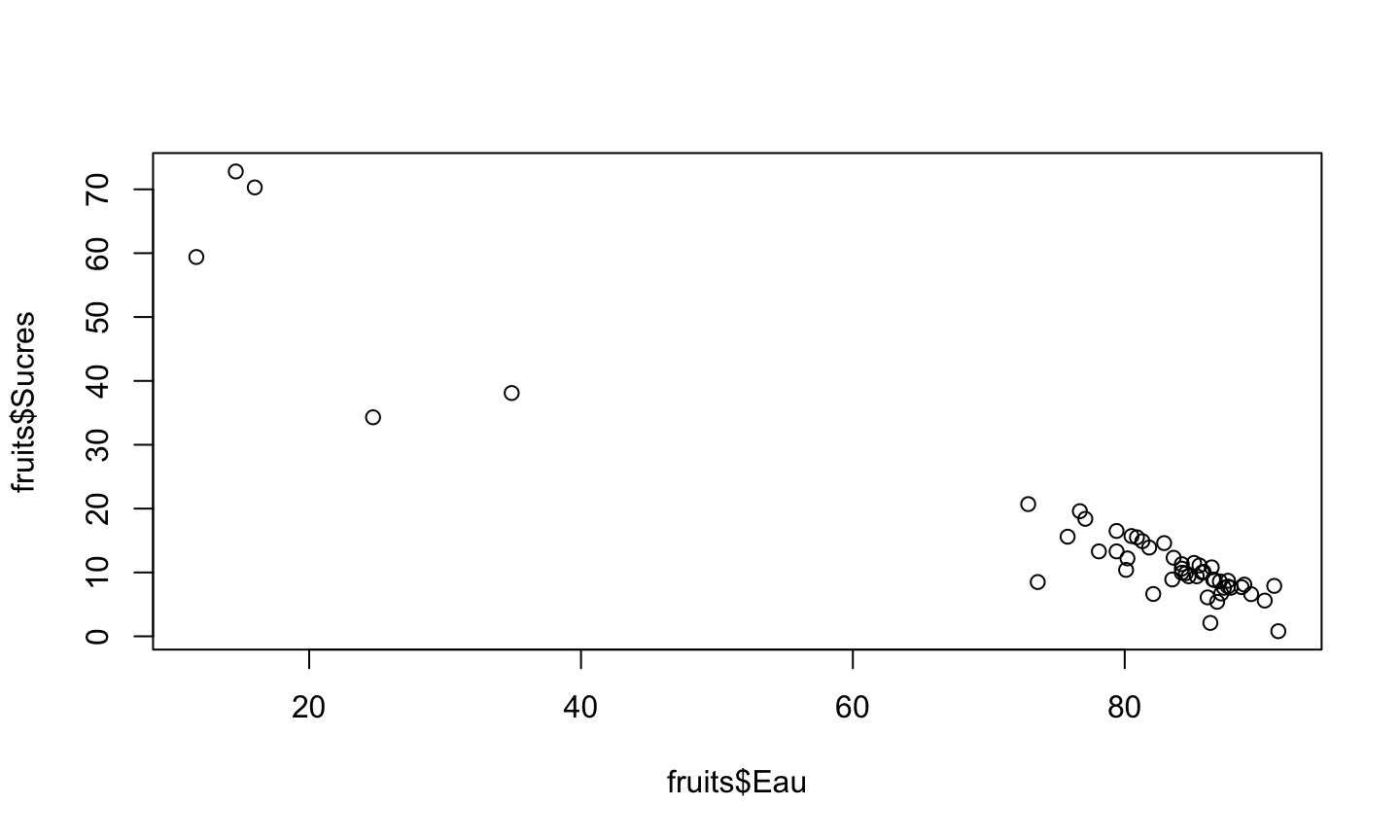
Permet de tracer des nuages de points :
plot(fruits$Eau, fruits$Sucres)
Exercice
Faire un histogramme de la teneur en Vitamine C des fruits crus.